I spend a lot of time reading articles on the internet and started wondering whether I could develop software to automatically discover and recommend articles relevant to my interests. There are various aspects to this problem but I have decided to concentrate first on the core part of the problem: the analysis and classification of the articles.
To illustrate the problem, lets consider the following string representing an article for the purpose of this example.
"the cunning creature ran around the canine"
We will attempt to use this article as a query to find similar or related articles from the following set of strings (usually referred to as a ‘corpus’), where each string also represents an article.
"The quick brown fox jumped over the lazy dog"
"hey diddle diddle, the cat and the fiddle"
"the fast cunning brown fox liked the slow canine dog "
"the little dog laughed to see such fun"
"and the dish ran away with the spoon"
The approaches we will consider for this example will work with any type of query equally whether the query is itself an article as above or simply a short string of words. The code used in this example is on Github and code demoing its use is included at the end of this blog post.
Term Frequency
One common approach is to capture the frequency with which each word (referred to as ‘term’) appears in each article (referred to as ‘document’), modelling each document as a numerical vector of term frequencies. The result is a term document matrix where each element tdi, j represents the frequency with which the corresponding term ti appears within the associated document dj. This is illustrated in the term document matrix below, constructed from our example corpus of articles.
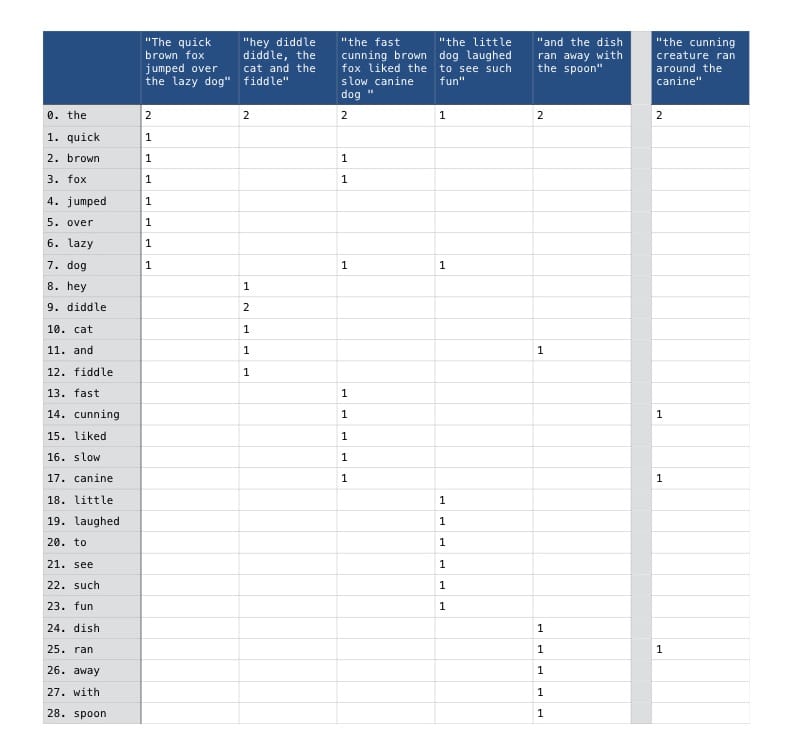
Values of 0 within the matrix, representing no occurances, have been shown as blank cells to aid readability. The column shown on the right of the matrix represents the article we are using as a query, included for comparison purposes.
It should be clear that that this matrix does not capture the sequence or proximity of words but rather simply their frequency regardless of where they appear in each document. A casual inspection of the values in the matrix should reveal that the third article the fast cunning brown fox liked the slow canine dog is the best match for our query having the most terms in common. This similarity can be confirmed by comparing the cosine similarity of each document in our corpus against the query.
Cosine similarity is a mathmatical measure of similarity between 2 numerical vectors that essentially calculates the difference between their angles. For a more in depth explanation of cosine similarity please refer to this article by Christian Perone. The calculated cosine similiarities will range from 0 (representing complete orthogonality) and 1 (representing a perfect match) with a higher cosine similarity value indicating greater similarity. Comparing our query with each of the document vectors yields the following results:

These results confirm our observations that the fast cunning brown fox liked the slow canine dog is indeed the closest match to our query.
Whilst this approach gave some success, there are a number of weaknesses. Re-examining the term document matrix, we can see that the second document hey diddle diddle, the cat and the fiddle had only one word in common with our query (the) and yet it scored a cosine similarity of 0.436436 because the word appeared twice in both the article and the query. In comparison, the first article The quick brown fox jumped over the lazy dog is semantically much more closely related to our query and yet it scores only a slightly higher cosine similarity. We shall tackle both these problems but lets start with the first: how to remove bias caused by words that occur frequently across the corpus e.g. the, a, and, etc.
TF-IDF (Term Frequency - Inverse Document Frequency)
One approach to solving this problem is to apply weightings to the term frequency values in the term document matrix. Words that appear frequently across the corpus will be given less weight than uncommon words so that they match less strongly. There are a number of formula available to do this, but one of the most common is tf-idf. In tf-idf, the inverse document frequency for each term is multiplied by the corresponding raw term frequency values in the matrix to yield a weighted tf-idf matrix. The formula for calculating tf-idf is as follows:
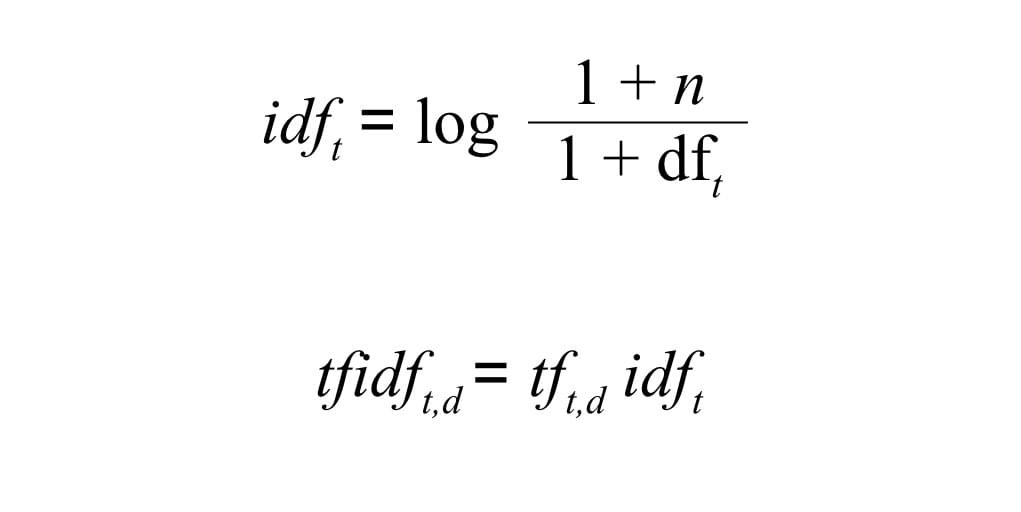
Where dft is the document frequency for a term i.e. the number of documents within which the term occurs and n is the total number of documents within the corpus. Both dft and n are added to 1 to remove the risk of dividing by 0. Using this formula, a term that appears in every document (e.g. the in our example corpus above) will be weighted down to 0 effectively cancelling itself out.
So, lets review our term document matrix after applying the tf-idf transformation.
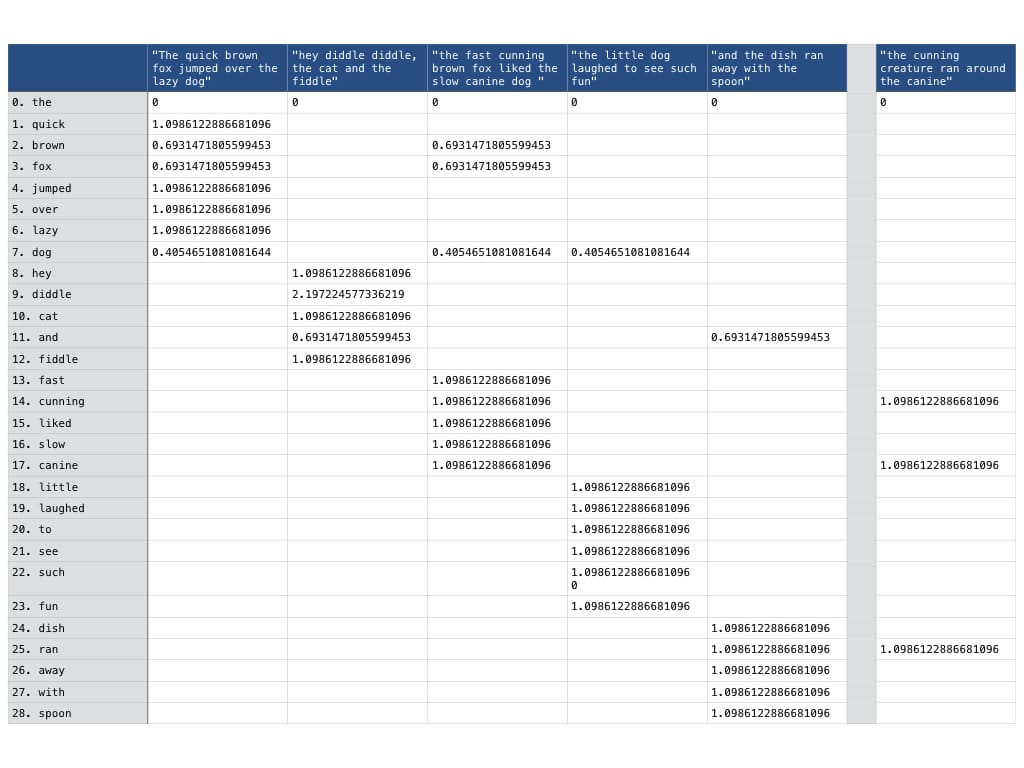
As theorised above, we can see that the word the has been cancelled out entirely, now scored as 0 in the term document matrix. Obviously, any transformation we apply to the documents within the corpus should also be applied to the query so that we are comparing like for like.
Now, lets see what effect the tf-idf transformation has had on our cosine similarity scores.

Looking at the new cosine similarity values we can see that only articles sharing words in common with our query are scoring non-zero cosine similarity. The tf-idf transformation removed the noise caused by commonly occuring words and has given us much cleaner and more marked results.
Latent Semantic Analysis
Whilst we are now getting clean similarity scores based on word occurance, we are still not matching semantically similar documents. For example, the first document The quick brown fox jumped over the lazy dog is semantically similar to our query - they are both about foxes and dogs. However, following tf-idf, this document now scores a cosine similarity of 0 because they have no words in common (beyond the word the which we weighted down by applying the tf-idf transform). So, how do we extract the semantic meaning hidden behind the term frequencies within the model? Enter Latent Semantic Analysis!
Latent Semantic Analysis (LSA) or Latent Semantic Indexing (LSI), as it is sometimes called in relation to information retrieval and searching, surfaces hidden semantic attributes within the corpus based upon the co-occurance of terms. It assumes that words that frequently occur together do so because they are semantically related to the same topic, concept or meaning. This is particularly important when analysing different words that mean the same thing, referred to as synonymy in natural language processing and allows documents to be considered similar even when they might not necessarily share any terms in common.
Latent Semantic Analysis relies on a mathematical process called truncated Singular Value Decomposition (SVD) to reduce the dimensionality of the term document matrix. Truncated SVD yields a new matrix that is the closest approximation to the original matrix within a significantly reduced dimensional space. For a more in depth explanation of the mathematics involed or internal workings of SVD please refer to the Golang code using SVD here and/or the material referenced at the end of the article. There are a number of advantages to the reduced dimensions as follows:
- The reduced dimensions should theoretically require less memory to store
- The act of truncating the least significant dimensions can reduce noise in the data leading to cleaner results
- Representing the document feature vectors in reduced dimensional space encodes co-occurance of terms and the hidden semantic meaning allowing matches between similar documents even with no terms in common.
For the purposes of this example, I shall project the tf-idf term document matrix into 2 dimensions as the initial dimensionality is relatively low anyway and 2 dimensions lends itself to visualisation (as we will see later). Usually in LSA, a value around 100 tends to yield the best results 2. Lets take a look at our matrix of feature vectors following SVD.
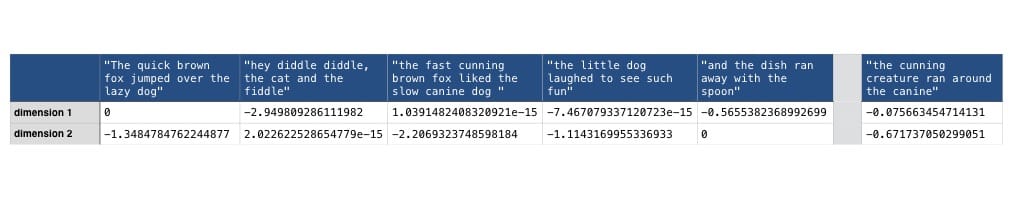
It should be clear that where we previously had a row for every term within the matrix, we now have only 2 dimensions to the matrix which represent the 2 dimensions of largest variation amongst the documents. As before, we must also project the query into the same dimensional space as the documents before we can compare them for similarity.
As the documents are now represented in 2 dimensions, it is possible to plot each document vector to help visualise clustering patterns in the documents. Lets take a look.
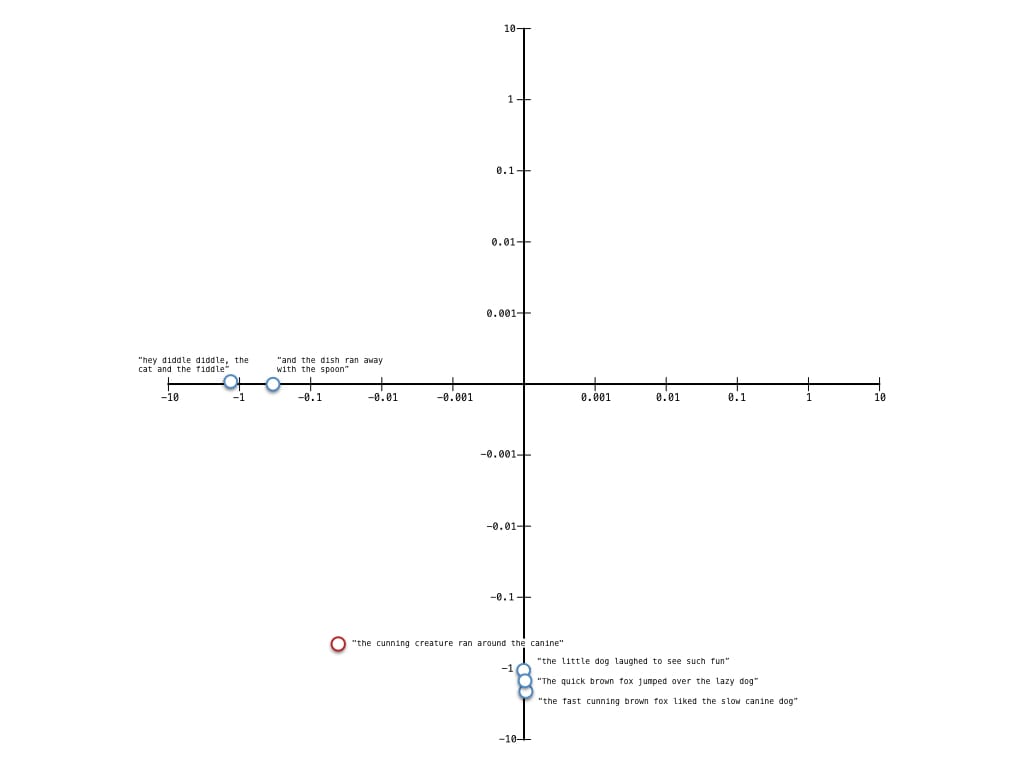
The saavy reader may have noticed that I have used logarithmic scales on both axis - this was to improve readability of the visualisation and make the angle between the query and other documents clearer. Looking at the plot, we can see that the documents have formed into 2 main clusters in this dimensional space. Those that are related to foxes and dogs, and those that are not. We can also see that the query is closer in angle (measured by a line from the origin to the point marked in the plot) to the cluster of documents relating to foxes and dogs which is exactly as it should be. Lets check the cosine similarities of the query with the document vectors in this dimensional space to check we are correct.

The cosine similarity scores support our observations from the plot. We can also see that our query "the cunning creature ran around the canine" strongly matches the document "The quick brown fox jumped over the lazy dog" even though they share no terms in common. The LSA has successfully resolved that they are both semantically related to foxes and dogs.
Go implement it (pun intended)
I have developed [Golang implementations for the machine learning algorithms described in this article and published them on Github][]. The implementations are based on papers and tutorials in the public domain and the structure of the code takes some inspiration from Python’s scikit-learn. Here is an example of how to use the library to output cosine similarities between the example query and document corpus used in this blog post following term frequency vectorisation, tf-idf transformation and SVD factorisation.
package main import ( "fmt" "gonum.org/v1/gonum/mat" "github.com/james-bowman/nlp" ) func main() { testCorpus := []string{ "The quick brown fox jumped over the lazy dog", "hey diddle diddle, the cat and the fiddle", "the fast cunning brown fox liked the slow canine dog ", "the little dog laughed to see such fun", "and the dish ran away with the spoon", } query := "the cunning creature ran around the canine" vectoriser := nlp.NewCountVectoriser(false) transformer := nlp.NewTfidfTransformer() // set k (the number of dimensions following truncation) to 2 reducer := nlp.NewTruncatedSVD(2) // Fit and Transform the corpus into a term document matrix fitting the // model to the documents in the process matrix, _ := vectoriser.FitTransform(testCorpus...) // transform the query into the same dimensional space - any terms in // the query not in the original training data the model was fitted to // will be ignored queryMat, _ := vectoriser.Transform(query) calcCosine(queryMat, matrix, testCorpus, "Raw TF") tfidfmat, _ := transformer.FitTransform(matrix) tfidfquery, _ := transformer.Transform(queryMat) calcCosine(tfidfquery, tfidfmat, testCorpus, "TF-IDF") lsi, _ := reducer.FitTransform(tfidfmat) queryVector, _ := reducer.Transform(tfidfquery) calcCosine(queryVector, lsi, testCorpus, "LSA") } func calcCosine(query mat.Matrix, tdmat mat.Matrix, corpus []string, name string) { // iterate over document feature vectors (columns) in the LSI and // compare with the query vector for similarity. Similarity is determined // by the difference between the angles of the vectors known as the cosine // similarity _, docs := tdmat.Dims() fmt.Printf("Comparing based on %s\n", name) for i := 0; i < docs; i++ { queryVec := query.(mat.ColViewer).ColView(0) docVec := tdmat.(mat.ColViewer).ColView(i) similarity := nlp.CosineSimilarity(queryVec, docVec) fmt.Printf("Comparing '%s' = %f\n", corpus[i], similarity) } }Wrapping up
We have looked at a number of ways to model text documents to support information retrieval each one building on the next. We started with modelling documents as feature vectors of raw term frequencies which we then extended with tf-idf weighting. We used tf-idf to weight the term frequencies according to how frequently the terms appeared across all the documents in the corpus thereby removing bias caused by commonly occuring words. Finally we extended the model with Latent Semantic Analysis, applying Singular Value Decomposition to surface semantic meaning hidden beneath the term frequencies within the document feature vectors.
I have really learnt a lot while implementing these algorithms both about machine learning concepts (and the requisite mathematics) and their applications. There are a number of extensions to the library that I intend to make both to extend my knowledge but also its usefulness including an implementation of LDA (Latent Dirichlet Allocation) for effective topic extraction from the documents and possibly also implementations of clustering and classification algorithms like k-means, etc.
If you have any experiences with using any of the algorithms I have described here or others that are related then please share your experiences in the comments section below.