In this blog post I will explore the steps to optimise a sparse vector dot product operation. We will start with a basic implementation in Go, convert it to assembler and then iteratively optimise it, measuring the effect of each change to check our progress. All the code from the post is available on Github and also forms part of the Golang Sparse matrix package.
A vector dot product is a very common kernel, or basic building block, for many computations used within scientific computing and machine learning e.g. matrix multiplication, cosine similarity, etc. The dot product simply multiplies together the respective elements of two vectors and then adds all the results together to give a scalar output.
Here is an example of how this operation could look in code.
func Dot(x []float64, y []float64) (dot float64) { for i, v := range x { dot += v * y[i] } return }1. Sparse Vectors
Sparse vector formats store only the non-zero values of the vector, supporting optimisations for both memory use and performance. This can yield significant gains in applications where the data is very sparse (mostly zeros) such as NLP (Natural Language Processing) and some machine learning applications. For example, in NLP it is common to have vectors where 99% of the elements as zero. A sparse vector therefore has 2 components: a float64 slice containing the non-zero values and an int slice containing the indices of those non-zero values. If we were to rewrite the example Dot function above so that one of the vectors, x, is sparse (with indx representing the indexes of the non-zero values) then it would look like this:
It should be clear from the code above that only the non-zero values of the sparse matrix x are being processed, multiplying them by their respective elements from the dense vector y. Multiplying the zero values of x by their respective elements of y would result in zero and so is redundant as it would not affect the overall dot product.
If we wished to calculate a dot product where both vectors are sparse, we can still use the above function but first scatter the values of one of the vectors into a dense vector so it can be supplied to the function as y.
To measure the performance of our function and establish a baseline, we will test it using Go’s built in benchmarking functionality. We will call the function with a number of different vector lengths to get a good feel of how the function performs over different inputs. We shall test with vectors of length 100, 1,000, 10,000 and 100,000. To keep the number of tests manageable, we will fix the density of the sparse vector to 10% (only 10% of the elements are non-zero).
Here are the results of the benchmark for our baseline Go implementation:
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000000 11.7 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot1-4 20000000 111 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot1-4 1000000 1179 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000 12640 ns/op
2. Assembly code
A full overview of programming assembler with Go is beyond the scope of this blog post. To implement our Dot funtion in assembler, we first need to define a prototype (the function definition, with no body) of the function within a .go file within the package as follows:
Next, we write the assembly code implementation of the function in a separate file with the suffix _amd64.s. It should be clear, this targets AMD64 compatible CPUs and if you wish to target an alternative CPU you would need to replace the amd64 substring in the suffix with the corresponding label for your CPU. Here is an initial, basic assmbler implementation of the sparse dot product function:
The first thing to note is the #include directive which should be familiar to anyone who has ever done any C/C++ programming. This include allows us to use human readable names for the function and branch labels within the code. Functions are always declared as TEXT ·Dot2(SB), NOSPLIT, $0 where Dot2 represents the function name and the value $0 indicates the size of the data frame. As we are not allocating any new memory - beyond what is passed into the function - we are using a size of 0 (the $ symbol denotes the 0 that follows it is a literal constant).
The first block of instructions moves the supplied function parameters into hardware registers so we can make use of them. Of note is the fact that the memory offsets into the data frame are required to address the parameters correctly. Slices are actually 24 bytes long and comprise 3 x 8 byte components:
- a pointer to the first element of the slice
- the length of the slice
- the capacity of the slice
You will notice at the end of the function, we move the result of the operation (the accumulator) from the register X0 back into the data frame so it can be accessed by the caller of the function.
The second block initialises the accumulator X0 and our loop index R9 by setting them to 0. It does this by XORing them by themselves as this is more efficient that explicitly setting them to 0.
The rest of the function should be fairly clear, there is a check to see if the loop index has reached the end of the vector (CMPQ R9, AX) and if it has, the next instruction (JGE end) jumps to the label end.
The next elements of indx and x are loaded into registers R10 and X1 accordingly and then the loop index i is incremented. The respective element of y (using the loaded value of indxin R10 to address it) is then multiplied by X1 and the result added to the accumulator X0.
Lets compare the performance of this assembler version against against the original Go implementation:
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000000 11.7 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000000 11.0 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot1-4 20000000 111 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot2-4 20000000 108 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot1-4 1000000 1179 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot2-4 1000000 1173 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000 12640 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000 12306 ns/op
The benchmark shows a modest improvement across the board. This is most likely due to the removal of the rather expensive implicit bounds checking that Go performs when accessing slices. There is no bounds checking in our assembler version.
3. Loop inversion
The first optimisation we will apply is called loop inversion optimisation. In essence, this optimisation exchanges the for loop from our original implementation for a do...while style loop where the condition is evaluated at the end of the loop. As we are now not evaluating the loop criteria until the end, we will also need to precede the loop with a conditional check to cover the case where the loop should run zero times.
We can see in the code above that the unconditional jump (JMP loop) instruction from our previous version Dot2 has been replaced with a conditional jump and the condition at the top of the loop has now been moved out of the loop entirely to precede it. This has reduced the number of branch/jump instructions followed by 2 and almost halving the number of branch instructions processed (both followed and un-followed). This is especially significant as branches are very expensive often causing execution pipeline stalls and branch mispredictions.
Lets review the benchmarks with our previous versions (Dot1 and Dot2):
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000000 11.7 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000000 11.0 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000000 10.9 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot1-4 20000000 111 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot2-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot3-4 20000000 107 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot1-4 1000000 1179 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot2-4 1000000 1173 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot3-4 1000000 1169 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000 12640 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000 12306 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000 12179 ns/op
As expected, we can see a modest improvement over the previous versions. This optimisation also allows us to now make further optimisations.
4. Loop reversal
The next optimisation is called loop reversal optimisation. Loop reversal, changes the order in which a loop iterates, typically decrementing the loop counter down towards zero rather than incrementing up from zero. The primary advantage is that the change can change data dependencies and enable other optimisations. This approach can also eliminate further loop overhead as many architectures support native jump if zero style instructions removing the need for the explicit CMPQ instruction to compare with 0 at the end of the loop.
It should be clear from the code that we have substituted a single SUBQ instruction for both the INCQ instruction incrementing the loop counter and the CMPQ instruction that preceded the conditional jump instruction at the end of the loop in the previous version. However, we have also added two additional ADDQ instructions to advance the pointers (SI and R8) through x and indx every iteration of the loop. As we are now using pointers to access the elements of x and indx rather than indexing with the loop counter, the addressing of the data looks much cleaner and will have lower overhead on some architectures.
Lets check the impact of our changes on performance.
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000000 11.7 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000000 11.0 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000000 10.9 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000000 11.6 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot1-4 20000000 111 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot2-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot3-4 20000000 107 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot4-4 20000000 108 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot1-4 1000000 1179 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot2-4 1000000 1173 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot3-4 1000000 1169 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot4-4 1000000 1169 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000 12640 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000 12306 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000 12179 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000 12251 ns/op
In all cases, this version performs slightly worse than the previous version. This is most likely caused by additional overhead due to advancing the 2 pointers, SI and R8. However, this change will allow us to now make other optimisations where we will realise the benefit.
5. Loop unrolling
To reduce the overhead from advancing pointers introduced in the previous optimisation, we will use Loop unrolling to spread this overhead and decrease the number of times it is executed. Loop unrolling (or loop unwinding as it is sometimes referred to) is a technique to reduce loop overhead by decreasing the number of times loop conditions are evaluated, pointer arithmetic is executed and the number of jumps (which are expensive). Simply put, the body of the loop is duplicated multiple times which in our case means processing multiple vector elements per iteration of the loop. For our use case we will unroll the loop 4 times i.e. duplicate the body of the loop 4 times and process 4 vector elements per loop iteration.
#include "textflag.h" // func Dot5(x []float64, indx []int, y []float64) (dot float64) TEXT ·Dot5(SB), NOSPLIT, $0 MOVQ x+0(FP), R8 MOVQ indx+24(FP), SI MOVQ y+48(FP), DX MOVQ indx+32(FP), AX XORPS X0, X0 SUBQ $4, AX JL tailstart loop: MOVQ (SI), R10 // indx[i] MOVSD (R8), X1 // x[i] MULSD (DX)(R10*8), X1 ADDSD X1, X0 MOVQ 8(SI), R10 // indx[i+1] MOVSD 8(R8), X1 // x[i+1] MULSD (DX)(R10*8), X1 ADDSD X1, X0 MOVQ 16(SI), R10 // indx[i+2] MOVSD 16(R8), X1 // x[i+2] MULSD (DX)(R10*8), X1 ADDSD X1, X0 MOVQ 24(SI), R10 // indx[i+3] MOVSD 24(R8), X1 // x[i+3] MULSD (DX)(R10*8), X1 ADDSD X1, X0 ADDQ $32, SI // SI += 4 * sizeOf(int) ADDQ $32, R8 // R8 += 4 * sizeOf(float64) SUBQ $4, AX // decrement loop counter by 4 JGE loop tailstart: ADDQ $4, AX JE end tail: // process any remaining elements if len(indx) is not divisible by 4 MOVQ (SI), R10 MOVSD (R8), X1 MULSD (DX)(R10*8), X1 ADDSD X1, X0 ADDQ $8, SI ADDQ $8, R8 SUBQ $1, AX JNE tail end: MOVSD X0, dot+72(FP) RETWe can see in the code above that we have repeated the instructions from the body of the loop 4 times, processing 4 elements per iteration of the loop. Each repeated instruction addresses the next vector element (+0, +1, +2, +3) and each iteration of the loop, the loop counter is decremented by 4 and the pointers are advanced by 4 elements. It should also be noted that we have replicated the loop, without unrolling, under the tail label. This is to handle vectors of lengths that are not exactly divisible by 4 - the tail section handles the remaining 1-3 elements after processing most of the elements in the main unrolled section.
Lets look at how this version compares with our previous benchmarks.
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000000 11.7 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000000 11.0 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000000 10.9 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000000 11.6 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot5-4 100000000 11.3 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot1-4 20000000 111 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot2-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot3-4 20000000 107 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot4-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot5-4 20000000 106 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot1-4 1000000 1179 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot2-4 1000000 1173 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot3-4 1000000 1169 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot4-4 1000000 1169 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot5-4 1000000 1189 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000 12640 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000 12306 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000 12179 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000 12251 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot5-4 100000 12388 ns/op
Whilst this appears to improve on our previous version in some cases, it is still slower than some of our earlier optimised versions. Many modern CPUs are able to achieve a degree of parallelism through out-of-order execution to make use of instruction cycles that would otherwise be wasted. By unrolling the loop we have created some additional dependencies within the loop which limit the amount of out-of-order execution. Unrolling the loop allows us to make other optimisations, and the next will address the dependencies we have created.
6. Software Pipelining
Using Software pipelining we can re-order the instructions to reduce the dependencies between adjacent instructions optimising for out-of-order execution.
#include "textflag.h" // func Dot6(x []float64, indx []int, y []float64) (dot float64) TEXT ·Dot6(SB), NOSPLIT, $0 MOVQ x+0(FP), R8 MOVQ indx+24(FP), SI MOVQ y+48(FP), DX MOVQ indx+32(FP), AX XORPS X0, X0 // Use 2 accumulators to break dependency XORPS X9, X9 // chain and better pipelining SUBQ $4, AX JL tailstart loop: MOVQ (SI), R10 // indx[i] MOVQ 8(SI), R11 // indx[i+1] MOVQ 16(SI), R12 // indx[i+2] MOVQ 24(SI), R13 // indx[i+3] MOVSD (R8), X1 // x[i] MOVSD 8(R8), X3 // x[i+1] MOVSD 16(R8), X5 // x[i+2] MOVSD 24(R8), X7 // x[i+3] MULSD (DX)(R10*8), X1 MULSD (DX)(R11*8), X3 MULSD (DX)(R12*8), X5 MULSD (DX)(R13*8), X7 ADDSD X1, X0 ADDSD X3, X9 ADDSD X5, X0 ADDSD X7, X9 ADDQ $32, SI ADDQ $32, R8 SUBQ $4, AX JGE loop tailstart: ADDQ $4, AX JE end tail: MOVQ (SI), R10 MOVSD (R8), X1 MULSD (DX)(R10*8), X1 ADDSD X1, X0 ADDQ $8, SI ADDQ $8, R8 SUBQ $1, AX JNE tail end: ADDSD X9, X0 // Add accumulators together MOVSD X0, dot+72(FP) RETWe can see in the code above, we have re-ordered the instructions in the main loop - effectively so that instructions dependent on other instructions appear further away from each other - this allows better instruction level parallelism through out-of-order execution within the CPU. We have also added an additional accumulator to reduce the dependencies when accumulating all of the element products. The two accumulators are added together at the end to form the final dot product.
Lets see the impact of our changes and compare with our previous benchmarks.
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000000 11.7 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000000 11.0 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000000 10.9 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000000 11.6 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot5-4 100000000 11.3 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot6-4 100000000 10.3 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot1-4 20000000 111 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot2-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot3-4 20000000 107 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot4-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot5-4 20000000 106 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot6-4 20000000 59.7 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot1-4 1000000 1179 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot2-4 1000000 1173 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot3-4 1000000 1169 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot4-4 1000000 1169 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot5-4 1000000 1189 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot6-4 2000000 746 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000 12640 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000 12306 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000 12179 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000 12251 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot5-4 100000 12388 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot6-4 100000 11971 ns/op
It should be clear from the benchmarks that this latest version is significantly faster than the others.
7. Vectorisation
The final optimisation we will apply is called Vectorisation. Vectorisation is a form of parallelisation where a scalar implementation (processing a single pair of operands at a time) is converted so that a single operation is applied to multiple pairs of operands simultanteously. This can be achieved through the use of SIMD (Single Instruction, Multiple Data) instructions which are supported on most modern commodity CPUs. Intel’s MMX, SSE and AVX extensions provide SIMD support.
#include "textflag.h" // func Dot7(x []float64, indx []int, y []float64) (dot float64) TEXT ·Dot7(SB), NOSPLIT, $0 MOVQ x+0(FP), R8 MOVQ indx+24(FP), SI MOVQ y+48(FP), DX MOVQ indx+32(FP), AX XORPS X0, X0 XORPS X9, X9 SUBQ $4, AX JL tailstart loop: MOVQ (SI), R10 MOVQ 8(SI), R11 MOVQ 16(SI), R12 MOVQ 24(SI), R13 MOVUPD (R8), X1 // Load x[i:i+1] into vector register MOVUPD 16(R8), X3 // Load x[i+2:i+3] into vector register MOVLPD (DX)(R10*8), X2 MOVHPD (DX)(R11*8), X2 MOVLPD (DX)(R12*8), X4 MOVHPD (DX)(R13*8), X4 MULPD X2, X1 // multiply 2 pairs of elements MULPD X4, X3 // multiply 2 pairs of elements ADDPD X1, X0 // add the pair of products to the pairs of accumulators ADDPD X3, X9 // add the pair of products to the pairs of accumulators ADDQ $32, SI ADDQ $32, R8 SUBQ $4, AX JGE loop tailstart: ADDQ $4, AX JE end tail: MOVQ (SI), R10 MOVSD (R8), X1 MULSD (DX)(R10*8), X1 ADDSD X1, X0 ADDQ $8, SI ADDQ $8, R8 SUBQ $1, AX JNE tail end: ADDPD X9, X0 // Add accumulators together MOVSD X0, X7 UNPCKHPD X0, X0 // Unpack vector register and ADDSD X7, X0 // add the 2 values together MOVSD X0, dot+72(FP) RETUsing Intel’s SSE extensions we can operate on pairs of elements at a time. Unfortunatly, due to the nature of sparse matrices, we are performing an implicit gather operation when loading elements from y. This means we have to load each element of y individually and then pack them, in pairs, into the SSE vector registers. In contrast, as we are processing the elements of x sequentially we can directly load the elements 2 at a time.
Lets compare the results with our previous benchmarks.
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000000 11.7 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000000 11.0 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000000 10.9 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000000 11.6 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot5-4 100000000 11.3 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot6-4 100000000 10.3 ns/op
BenchmarkDot/10/100_github.com/james-bowman/algos/sparse/dot.Dot7-4 200000000 9.14 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot1-4 20000000 111 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot2-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot3-4 20000000 107 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot4-4 20000000 108 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot5-4 20000000 106 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot6-4 20000000 59.7 ns/op
BenchmarkDot/100/1000_github.com/james-bowman/algos/sparse/dot.Dot7-4 30000000 43.4 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot1-4 1000000 1179 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot2-4 1000000 1173 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot3-4 1000000 1169 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot4-4 1000000 1169 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot5-4 1000000 1189 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot6-4 2000000 746 ns/op
BenchmarkDot/1000/10000_github.com/james-bowman/algos/sparse/dot.Dot7-4 2000000 701 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot1-4 100000 12640 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot2-4 100000 12306 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot3-4 100000 12179 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot4-4 100000 12251 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot5-4 100000 12388 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot6-4 100000 11971 ns/op
BenchmarkDot/10000/100000_github.com/james-bowman/algos/sparse/dot.Dot7-4 200000 11648 ns/op
We can see from the benchmarks that this optimisation has yielded further performance gains.
Wrapping up
Reviewing the benchmarks we can see that in most cases, each optimisation provided incremental gains over the last. In some cases however, certain optimisations actually resulted in a performance decrease. This is because for some optimisations, the benefits are only realised when combined with other optimisations or are important because they open the door for other optimisations that would not have been possible otherwise.
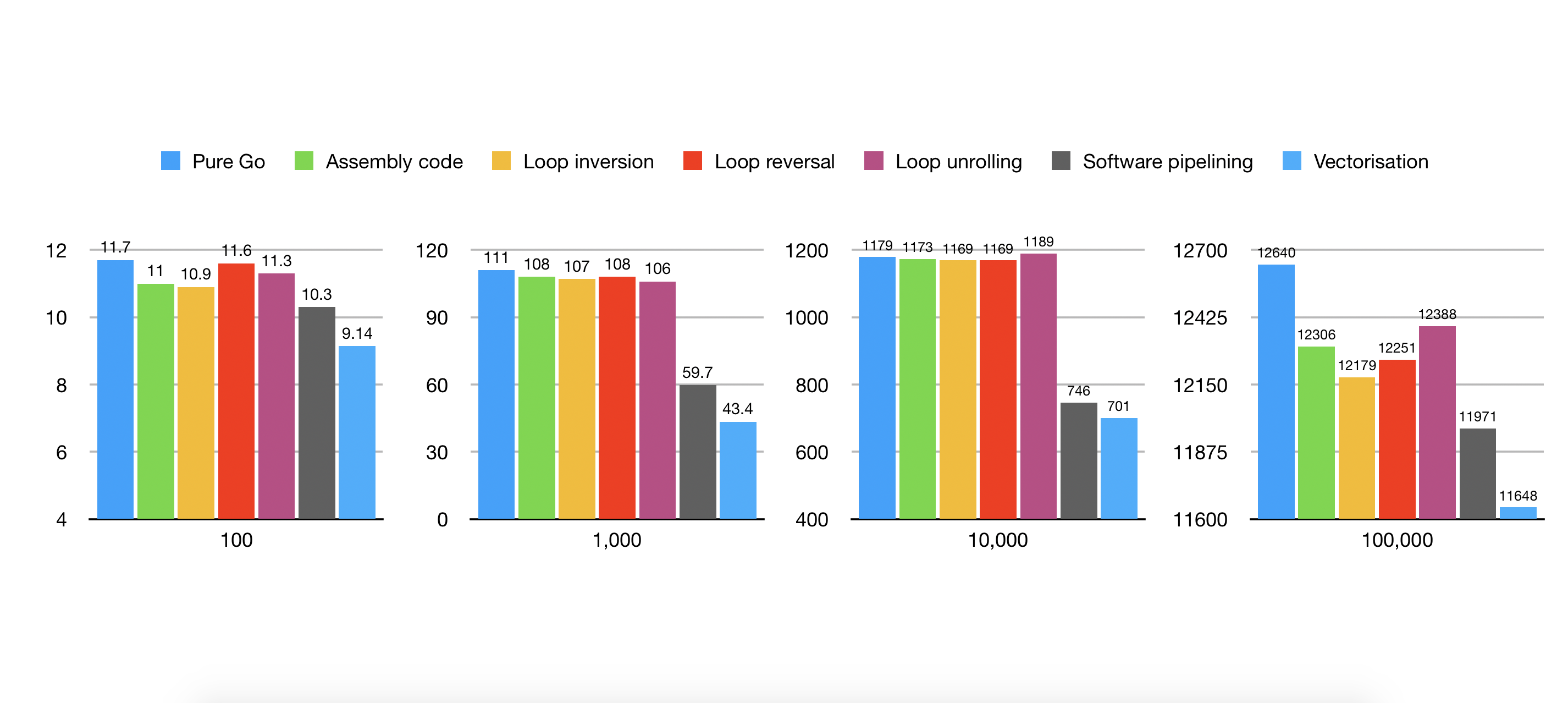
The cumulative effect of all our optimisations is significantly faster than the original Golang version. Where this function is used as a basic building block for other operations e.g. the inner loop of matrix multiplication, this improvement is effectively multiplied and will have an even bigger impact on performance. It is however worth bearing in mind that these performance gains come at the cost of additional complexity, there is more code that is relatively complex and so harder to maintain. This trade-off should be considered carefully when choosing to optimise code in this way. It is also worth considering that some of these optimisations may work better or worse on specific CPU architectures so your mileage may vary.